A local energy community (LEC) is a set of residential or small industrial sites each acting as a prosumer, being equipped, in general, with generation units, battery energy storage (BES) units and loads. All the prosumers are connected to the same low-voltage (LV) distribution network, which is the internal network of the LEC and it is connected to the medium-voltage (MV) external utility grid.
In a LEC, each prosumer uses the available energy resources in cooperation with the others to minimize the energy procurement costs. Due to the difference between the price of the energy supplied by the utility grid and the price paid to the local energy production, the power exchanges with the utility grid are reduced.
The operation of a LEC needs the implementation of an energy management system (EMS) for the optimal scheduling of the available resources [1]. This post focuses on an algorithm for the day-ahead scheduling of the BES units. We assume that all the generation units of the LEC are photovoltaic (PV) panels and the effects of power loss in the internal network can be neglected.
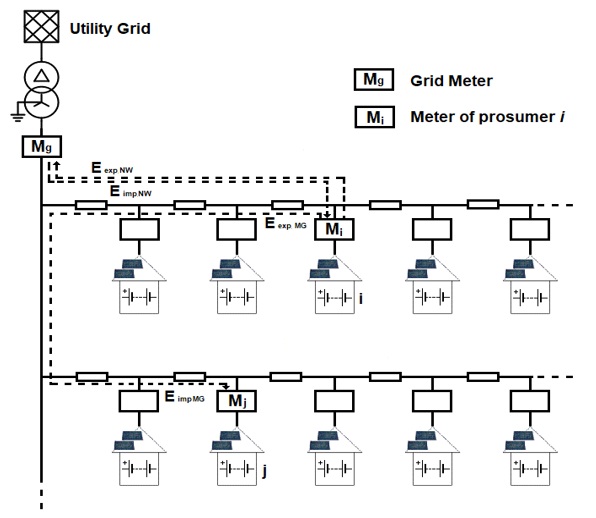
Figure 1. Scheme of the LEC
Fig. 1 illustrates a LEC scheme. The point of common coupling (PCC) with the utility grid is represented by the LV side of the distribution transformer. The grid meter Mg, positioned at the PCC, is bidirectional to measure the net energy exchanged by the LEC with the utility grid in each time interval (bought or sold).
Typical Centralized Approach - Mixed Integer Linear Programming model
The centralized approach, in which a central control unit performs the entire optimization, implies that the prosumers communicate all the details of the equipment features as well as the load and production forecasts.
Under these conditions, the typical Objective function (OF), minimizes the total cost associated with the power exchanged with the utility grid where:
πbuy and πsell, are the prices (in €/kWh) of the energy bought from and sold to the utility grid; Pbuy_grid and Psell_grid are the average power bought from and sold to the utility grid (in kW) in time interval t; Δt is the time step of the optimization problem.

With the coupling constraint equilibrium between the energy bought from producer i by the other prosumers and the energy sold by producer i, and other operational constraints for each prosumer, for instance:
- power balance for the i-th prosumer
- avoid simultaneous purchase and selling by the same prosumer
- model of the BES units
Distributed procedure to solve the scheduling problem of local energy communities
In order to preserve, as much as possible, the confidentiality of the features and forecast of prosumers’ equipment, the problem can be addressed by designing a specific distributed procedure based on the alternating direction method of multipliers (ADMM).
The distributed procedure provides the scheduling of the batteries to limit the balancing action of the external grid. With respect to a centralized approach, the adoption of distributed approaches, as the ADMM, is preferable for the solution of the problem considered, since it reduces the need for each prosumer to communicate all the features and forecasts of the its own units and loads to the other prosumers or to a coordinating unit (e.g [2]–[5]). Furthermore, the distributed approach is compatible with the adoption of a distributed ledger technology (DLT).
ADMM is one of the most frequently adopted consensus methods [6] and it has been recently investigated also for the solution of scheduling problems in microgrids (e.g., [7], [8], and references therein). In particular, both [7] and [8] deals with similar multi-microgrid systems as the one considered in this paper, with the presence of local generation, BES units and the possibility to exchange energy with an external utility grid. Moreover, [8] addresses the uncertainty of renewable energy, load consumption, and energy prices through a robust optimization approach.
The optimization is iteratively carried out by each prosumer k. At each ADMM iteration, the energy bought or sold by each prosumer in every time t is made known to all the prosumers.
The objective function of prosumer k is

Where

OFk can be seen as the summation of the costs of the energy bought by prosumer k from the utility grid at price πbuy and from the other prosumers at prices λj minus the sum of the revenues due to the energy sold by prosumer k to the utility grid at price πsell and to the other prosumers at price λk.
Fig. 2 presents a diagram of a proposed implementation of the ADMM algorithm, with the following characteristics:
- at the beginning of the ADMM procedure, prices λk and scaling factor m are initialized;
- at each iteration ν, after the solution of the optimization problem, prosumer k communicates both Pbuy k,j and Psell k,j to every other prosumer j. When all the prosumers have solved their own optimization problems, they update Lagrangian multipliers λk and penalty parameter ρ. For this purpose, the primal and dual residual terms are calculated;
- the procedure is repeated until the absolute value of each residual becomes equal or lower than tolerance ε
- To accelerate the convergence, the initial value of m is multiplied by 10 when the maximum value of the total mismatch becomes lower than 1 kW, and further multiplied by 10 when (adjustable values according to the case study).
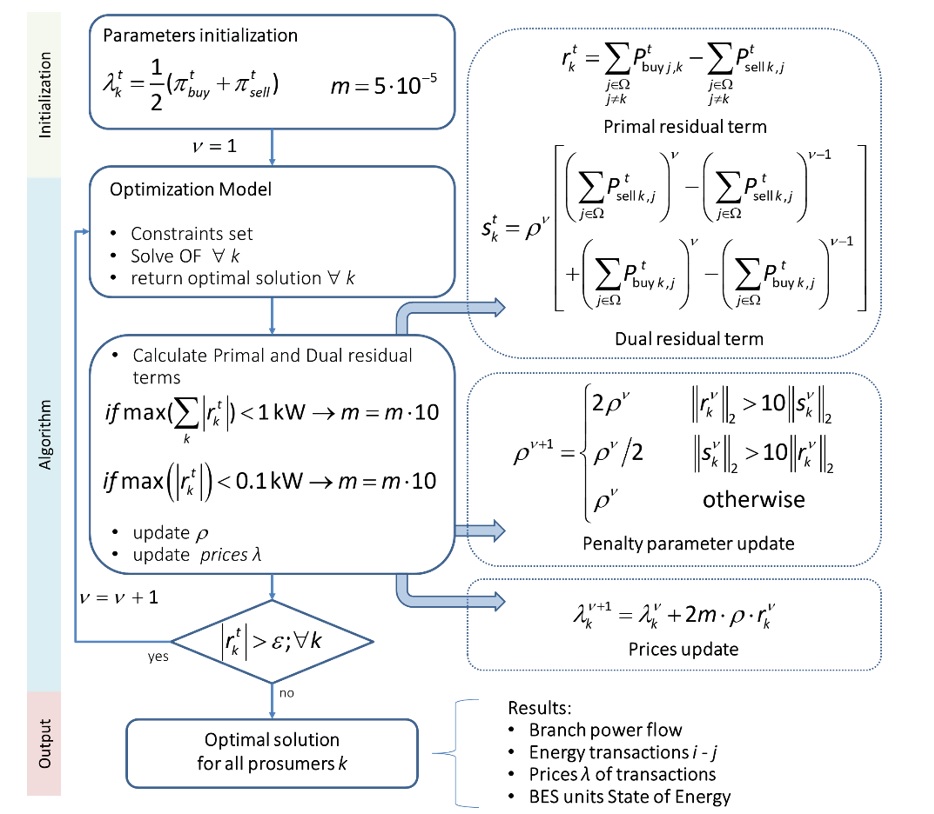
Figure 2. Proposed ADMM procedure
Once the procedure converges, the additional term is zero and the value OF for the whole system is the sum of the ones solved for each prosumer k:

Comparison between the solution of the distributed procedure and the centralized approach
Both the centralized approach and distributed one allow the effective scheduling of the storage systems owned by the various prosumers.
Now, we compare the solutions obtained by applying the centralized and the distributed models for both a case study with the BES units and the one without BES units.
- Profiles of the power exchanger with the utility grid
The comparison between the profiles of the power exchanged with the utility grid is shown in Fig. 3. As expected, the profiles are quite similar. This is reflected in OF values pretty similar for the two approaches.
The profiles of the power exchanged with the utility grid obtained by using the centralized and the distributed approach: a) without BES units (left graph) and b) with BES units (right graph). Positive values indicate imported power from the utility grid, negative values indicate exported power to the utility grid.
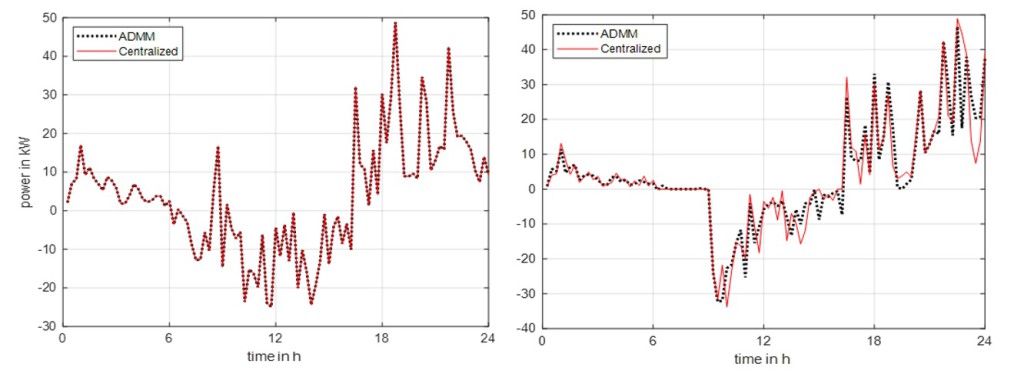
Figure 3. The profiles of the power exchanged with the utility grid obtained by using the centralized and the distributed approach: a) without BES units (left) and b) with BES units (right)
- Energy in the BES Units
The energy stored in the batteries provided by the distributed approach are in close agreement with those calculated by the centralized one (See Fig. 4).
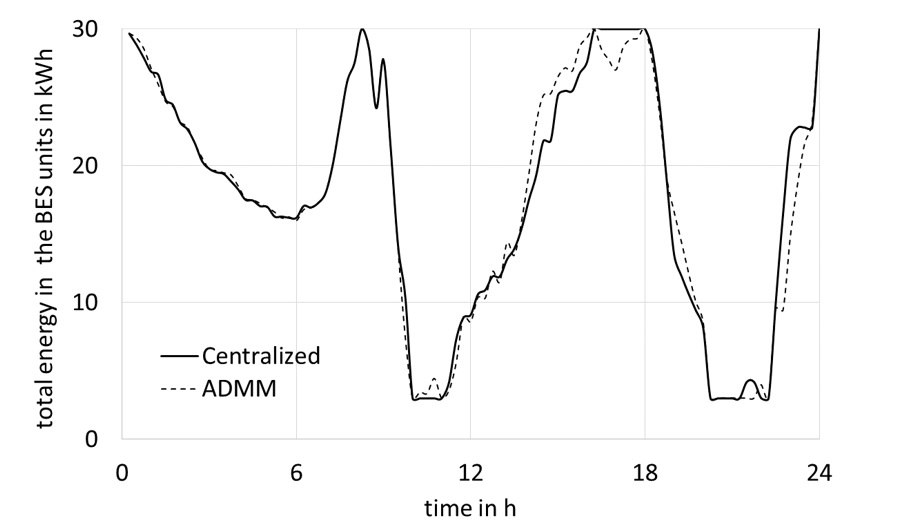
Figure 4. Comparison of the total energy in the batteries of the LEC obtained by the centralized and the distributed approach
Conclusions
The results obtained by using the proposed distributed optimization procedure based on the application of the alternating direction method of multipliers have been compared with those from a centralized approach based on a mixed integer linear programming model. The distributed approach has the advantage to reduce the information that each prosumer must share with the other prosumers.
We summarize the main results in the following points:
- Both centralized approach and the distributed one provide comparable results with an acceptable computational effort.
- The values of the objective function, the profiles of the power exchanged with the utility grid and the profile of the energy stored in the batteries match.
- In the distributed procedure, the prices are updated at each iteration to reduce the mismatch between the energy sold by each prosumer i and the energy bought by the other prosumers from prosumer i. Notwithstanding these differences, the profiles of the prices are similar for both the cases with and without BES units.
- The structure of the day-ahead scheduling procedures is consistent with the billing scheme and the metering units of the LEC.
- For each prosumer, the results confirm the cost reduction or revenue increase in the LEC compared to the case in which it can only transact with an external energy provider.
References
[1] B. Prasad, E. Koliou, J. Friege, R. A. Hakvoort, and P. M. Herder, “Energetic communities for community energy : A review of key issues and trends shaping integrated community energy systems,” Renew. Sustain. Energy Rev., vol. 56, pp. 722–744, 2016. [2] M. Luisa, D. Silvestre, P. Gallo, M. G. Ippolito, and E. R. Sanseverino, “A Technical Approach to the Energy Blockchain in Microgrids,” IEEE Trans. Ind. Informatics, vol. 14, no. 11, pp. 4792–4803, 2018. [3] C. Long, J. Wu, C. Zhang, L. Thomas, M. Cheng, and N. Jenkins, “Peer-to-peer energy trading in a community microgrid,” in 2017 IEEE Power & Energy Society General Meeting, 2017, pp. 1–5. [4] A. Paudel, K. Chaudhari, C. Long, and H. Gooi, “Peer-to-Peer Energy Trading in a Prosumer Based Community Microgrid : A Game-Theoretic,” IEEE Trans. Ind. Electron., vol. PP, no. c, p. 1, 2018. [5] Y. Zhao, J. Yu, M. Ban, Y. Liu, and Z. Li, “Privacy-preserving economic dispatch for an active distribution network with multiple networked microgrids,” IEEE Access, vol. 6, pp. 38802–38819, 2018. [6] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers. Now Foundations and Trends, 2011. [7] Y. Zheng, Y. Song, D. J. Hill, and Y. Zhang, “Multiagent system based microgrid energy management via asynchronous consensus ADMM,” IEEE Trans. Energy Convers., vol. 33, no. 2, pp. 886–888, 2018. [8] Y. Liu, Y. Li, H. B. Gooi, J. Ye, H. Xin, X. Jiang, and J. Pan, “Distributed robust energy management of a multi-microgrid system in the real-time energy market,” IEEE Trans. Sustain. Energy, vol. 3029, no. vol. in print, pp. 1–11, 2018.

